じゃんけんグリコを題材にしてExcelで遊ぶシリーズ
なんか新しいことでもやろうかということで、部屋の本棚を色々とあさっていると、進化ゲーム理論と遺伝的アルゴリズム―「協調」と「対立」のシミュレーション (I・O BOOKS)なる本を見つけた。
どういう意図で購入したのかは今となっては思い出せないのだけれど、なんとなく面白そうなのでこれを利用して、何か遊べたらいいよねということで早速やってみることにした。今回使用したのは、いつものWindowsPCとExcel2007である。
題材と探索の旅
この本で書かれているのは、囚人のジレンマを出発点として、表題の話をつなげていくというものである。で、その話を進めていく上で、Excelを使用しているという寸法である。
なんか、おもしろそうやねというのはいいとして、いくらなんでも同じことをやっても仕方がない。じゃあ、何か題材がないかなあと探してみると、何か良さげな奴がありましたぞと。
いわゆる、相手とじゃんけんをしてグーで勝つと3歩進めて、チョキかパーで勝つと6歩進めるゲームである。おそらく子供の頃、一回は遊んだ事があるであろう、この遊びである。
チョキとパーは6歩なのに、グーだけは3歩という、この不公平感。そして、あからさまな1粒で300m臭。なんか、ゾクゾクわくわくするよねということで、色々とサイト探索の旅へ。
今だからこそもっと楽しめる!大人の社会見学へ出かけよう!
Wikipedia:グリコ (遊び)
空気を読まない中杜カズサ:「チョコレート」「パイナップル」「グリコ」は今考えるとかなり深いと思う話
教えて!goo:じゃんけん(グリコ・チョコレート・パイナップル)の最適値?
じゃんけんグリコの最適戦略を探る
「じゃんけんグリコ」の数学
ジャンケンで探るゲーム理論入門
色々と見ていくと、このゲームは、通称として「じゃんけんグリコ」とされているようだ。で、どうやら、負けない手としては、グー:チョキ:パーの割合が、2:2:1で出せばいいような感じのことが、とっくに調べられていたのであった。
ああ、Excelでいつものインチキ術を使って、負けない手を調べてみるために悪戦苦闘する様子を、記事投稿することで、ページを増産する予定だったのに、いきなり出鼻をくじかれてしまったのだった。
ハサミはちょっとだけお得?
そこで、例の本を色々と眺めてみる。すると、第2章にて、ちょっと楽しそうなモデルが書かれていた。3つの戦略が試合をして獲得できる平均利得表から、得点の高い戦略は仲間を増やしていき、得点の低い戦略は仲間が減っていくというもののモデルである。
詳しい内容は本を買ってねと宣伝したところで、この話を、今回のじゃんけんグリコに当てはめてみようと思う。
ということで、利得表を作ってみた。

図1.利得表(あいこ0ベース)
左のカラムが自分が出す手で、上カラムが相手の手になる。
自分がグーに対して、相手がグーなら、引き分けなので利得は0。相手がチョキなら、自分は3歩進めるので利得は3。相手がパーなら、相手が6歩進むので、自分としては6歩損なので利得は-6という感じである。
ただ、これだと後に作ろうとした表でdiv/0を食らってしまったので、ちょっと変えてみる事にした。

図2.利得表(あいこ6ベース)
単に、図1の利得表を全体的に+6しただけのことである。
ここで、なんとなーくわかるのは、本来じゃんけんといえば三すくみみたいな形になるのだけれど、グーは3歩しか進めないという特異性により、チョキさんはグーには負けるけれども、他の負けの関係よりはちょっと有利かも?という状態になっていることがわかる。
総当たり戦を繰り返すだけのお仕事です
さて、今回やるのは、あらかじめグー軍団と、チョキ軍団と、パー軍団の第0世代の初期人数と合計数(合計数はずっと固定)を決めて、各人が(自分を含めて)総当たり戦を行ったとして、その各軍団で得られた利得の合計から、次の第1世代の人数が決定するという作業をひたすら繰り返していくと、どうなっちゃうの?というのをやってみるのだ。
今回、例えば、各軍団が1,000人ずついるとする。
すると、グー軍団の1人と、自分を含めた計3,000人との勝負になるわけだ。結果として、図2の左カラムのグー欄の1,000倍したものの合計が、その1人の利得になるわな。
6×1,000人+9×1,000人+0×1,000人=15,000。これが1000人いるので、結果、グー軍団の合計点は15,000,000
同様に、チョキ軍団は、1人当たりは21,000で、合計21,000,000、パー軍団は1人当たり18,000で合計18,000,000となる。
各軍団の得点の合計は、54,000,000で、3軍団の合計3,000人で割ると、1人平均は18,000。この数値と、各軍団の1人当たりの利得を比較すると、グーは83.33%、チョキは116.67%、パーは100.00%となる。
この結果、第1世代では、グー軍団は1,000人×83.33%=833.3人、チョキ軍団は1,166.6人、パー軍団は1,000人になり、以下、その繰り返しで軍団の人口推移を見ていこうという話なのである。
グーの天下
人口推移をグラフにしてみた。
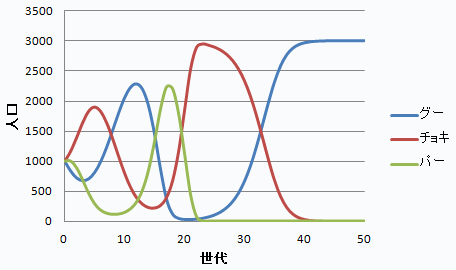
図3.各1,000人としたときの推移
最初のうちは、どこからでも得点が取れるチョキ軍団が有利。第5世代においてチョキ軍団1,903人という状況になる。すると、チョキに比較的強いグー軍団が伸びてくる。第12世代において、グー軍団は2,281人へ。
すると、パーが盛り返してくる。グーを食らうパー軍団の天下へ。そうなってくると、チョキ軍団はまた伸びてくる。第17世代において、パー軍団が2,236人だったものが、どんどん減っていくはめに。こうしてパー軍団の天下になるかと思いきや、第21世代において、24人にまで減らしていたグー軍団が息を吹き返してきた。
というのは、グーの天敵のパー軍団が、第24世代において0.1人へ、第25世代においては、0.004人という、要するに滅亡状態になっちゃったのね。
ってことで、だいたい第46世代あたりで、チョキ軍団もほぼ滅亡して、グーの天下になっちゃったわけだ。
2:2:1
じゃあ、この割合で出せば良いということで、グー:チョキ:パー=2,000人:2,000人:1,000人でやってみた。
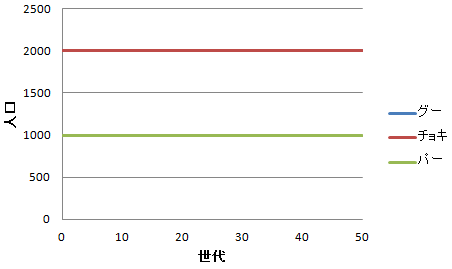
図4.2:2:1にしたときの推移
※グーとチョキの線は重なっているのに注意
すると、おお人口がぜーんぜんうごかない。どの軍団も平和に暮らしましたとさ。ちゃんちゃん。
やっぱり、この配合比はすごいのね。というのはさておき、今後、気が向いたら、このExcelで遊ぼうシリーズは続けていく予定。
工学社
売り上げランキング: 588,255
Pick Up
-
 1
1 -
Macbook air Mid2012 のバッテリー交換を行おうとして右往左往したときのログ(前編)
やったときのログシリーズ、バッテリー交換編
-
 2
2 -
Macbook Air Mid2012 のバッテリー交換をしたときのメモ(後編)
バッテリー交換後編。

